
""" # unpack the model parameters from the tuple m, c = theta # evaluate the model (assumes that the straight_line model is defined as above) md = straight_line ( x, m, c ) # return the log likelihood return - 0.5 * np. Args: theta (tuple): a sample containing individual parameter values data (list): the set of data/observations sigma (float): the standard deviation of the data points x (list): the abscissa values at which the data/model is defined Note: We do not include the normalisation constants (as discussed above).
#ABSCISSA EXAMPLE PLUS#
inf # return the likeihood times the prior (log likelihood plus the log prior) return lp + loglikelihood ( theta, data, sigma, x ) def loglikelihood ( theta, data, sigma, x ): """ The natural logarithm of the joint likelihood. Args: theta (tuple): a sample containing individual parameter values data (list): the set of data/observations sigma (float): the standard deviation of the data points x (list): the abscissa values at which the data/model is defined """ lp = logprior ( theta ) # get the prior # if the prior is not finite return a probability of zero (log probability of -inf) if not np. """ from _future_ import print_function, division import os import sys import numpy as np # import emcee import emcee # import model and data from createdata import * def logposterior ( theta, data, sigma, x ): """ The natural logarithm of the joint posterior. The mathematician Rene Descartes and Pierre de Fermat invented analytic geometry in 16th century and Cartesian plane was designed.Ģ.#!/usr/bin/env python # -*- coding: utf-8 -*- """ Example of running emcee to fit the parameters of a straight line. Geometric shapes like circle, triangle, square, rectangle and polygons use the ordered pairs to represent the center, vertices and the length of the sides with coordinates.ġ. The coordinate geometry uses ordered pairs to represent geometric figures and objects in an open space for visual comprehension.The concept of ordered pair is highly useful in data comprehension as well for word problems and statistics.Both represent two different points as shown below. The ordered pair (6, 4) is different from the pair (4, 6). From here, take 4 steps towards the “y” axis (upwards).Īs the name “ordered pair” suggests, the order in which values are written in a pair is very important. Take 6 steps towards the “x” axis (towards right) starting from the origin. To mark the point on the Cartesian plane, start from the origin. The second number in the ordered pair shows the distance from “y” axis which is 4.The first number in the ordered pair shows the distance from “x” axis which is 6.Plot the point “P” with coordinates 6, 4.Īs per the definition of ordered pair, the point P will be written as:
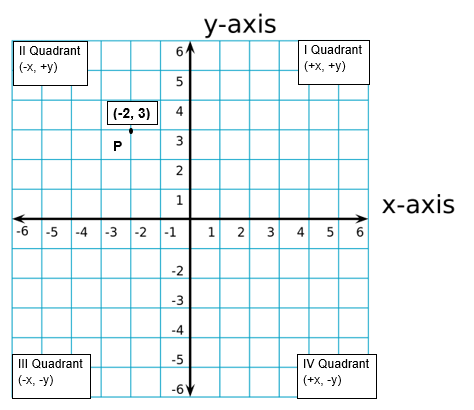
To comprehend it better, let’s take an example.

The point where the two lines meet at “0” is the origin. In the Cartesian plane, we define a two-dimensional space with two perpendicular reference lines, namely x-axis and y-axis. Where, x = abscissa, the distance measure of a point from the primary axis “x”Īnd, y = ordinate, the distance measure of a point from the secondary axis “y” The numeric values in an ordered pair can be integers or fractions. It helps to locate a point on the Cartesian plane for better visual comprehension. An ordered pair is a composition of the x coordinate (abscissa) and the y coordinate (ordinate), having two values written in a fixed order within parentheses.


 0 kommentar(er)
0 kommentar(er)
